Выберите правильный вариант ответа. К какому типу принадлежит последовательность |an|, заданная формулой n–го члена An=(-2)n?
+ a. Неограниченная
b. Возрастающая
c. Ограниченная
d. Убывающая
рЕШЕНИЕ
ТЕСТОВ и практических заданий
!!!! ИНФОРМАЦИЯ 2025 год
Расписание ликвидации академических задолженностей
за весенний семестр 2024/2025 учебного года.
Первая с 01.09.2025 г. по 14.09.2025 г.
Вторая с 01.11.2025г. по 09.11.2025г
Сдача (решение) одного теста по данному предмету - от 150 руб.
Список некоторых вопросов из тестов, на которые мы можем помочь с ответами.
• Выберите правильный вариант ответа. При каком условии функция f(x) имеет устранимый разрыв в точке c ?
• Выберите правильный вариант ответа. К какому типу принадлежит последовательность |an|, заданная формулой n–го члена An=(-2)n?
• Пусть функция y=f(x) дважды дифференцируема. Установите соответствие между характеристиками функций и необходимыми условиями, наложенными на эти функции:
• Укажите сходимость ряда при заданном условии. Ряд
• Установите соответствие между графиками функций y=f(x) и характеристиками этих функций:
• Установить соответствие между интегралом и его значением:
• Выберите вид производной функции
• Установите соответствие между пределами и их значениями:
• Укажите, чему равен градиент функции в точке максимума.
• Найдите число элементов пересечения множеств N∩K, если N={31, 32, 34, 35} и K={30, 34, 35, 36}.
• Выберите правильный вариант ответа. Определить точки разрыва функции, указать какого они типа
• Установите соответствие между пределами функций и типом неопределенности:
• Установите соответствие между графиками функций y=f(x) и их производными y'=f' (x):
• Укажите условие сходимости обобщенного гармонического ряда
• Укажите, чему равен дифференциал постоянной функции.
• Найдите и запишите производную функции в точке x=1
• Найдите число элементов разности множеств А \ В, если А={1; 2; 4; 6; 8; 10} и В={0; 2; 4; 8; 9}
• Установите, чему будет равен предел , если известно, что
• Выберите правильное выражение производной функции
• На рисунке изображен график функции y=f(x)
• Вычислите производную функции y= -20
• Установить соответствие между неопределенными интегралами или производной с их значением:
• Вычислите значение f(1), если f(x) – такая функция, что F(x)= x3 +5x+1 является ее первообразной.
• Выберите выражение, которое соответствует второй частной производная z " xy для функции z=xy 2 +e x .
• Установите, чему будет равен предел , если известно, что
• Выберите из данных рядов сходящиеся. Укажите несколько вариантов.
• Выберите вид производной функции
• Установите соответствие между видом функции и её названием:
• Установите соответствие между пределами и их значениями:
• Укажете формулу «первого замечательного предела»
• Выберите правильный вариант ответа. Пересечение множеств А и В – это...
• Вычислите значение несобственного интеграла
• Укажите, каким должен быть предел последовательности частичных сумм ряда, чтобы ряд назывался сходящимся.
• Установить соответствие между функцией и определением ее на четность.
• Вычислите значение F(5), если F(x) – первообразная функция от f(x)=2x-5. Первообразная удовлетворяет условию F(0)=0
• Установить соответствие между функцией и характером разрыва в точке x=0:
• Установите соответствие между функциями и их разложениями в степенные ряды:
• Установите соответствие между функциями и характеристиками этих функций:
• Установите соответствие между графиками функций y=f(x) и их производными y'=f' (x):
• Укажите, какие из перечисленных функций бесконечно малые при x→0: (укажите несколько вариантов)
• Вычислите предел функции
• Установите, чему будет равен предел если известно, что
• Вычислите производную функции y=5x-2
• Вычислите значение второй производной в точке x0=1 функции y = x5 – x4 + x3 – x2 + x – 5
• Указать метод интегрирования при вычислении неопределенного интеграла:
• Установите соответствие между функциями и характеристиками этих функций на отрезке [0; 1]:
• Укажите сходимость ряда при заданном условии. Ряд при limn→ ∞un=0
• Вычислите значение третьей производной в точке x0=1 функции y = x5 – x4 + x3 – x2 + x – 5
• Вычислите значение несобственного интеграла
• Установите соответствие между функциями и характеристиками этих функций:
• Укажите значение производной функции в точке f ’(x0), которое является условием экстремума дифференцируемой функции f(x) в точке x0
• Выберите правильный вариант ответа. Указать числовой промежуток, на котором определена функция
• На рисунке изображен график функции y=f(x)
• Установите соответствие между точкой x i и непрерывностью функции в этой точке:
• Непрерывная двумерная случайная величина распределена внутри прямоугольного треугольника с вершинами О (0;0), А(0;14), В(14;0). Найти плотность системы.
• Найти угол между векторами a и b a = {3; 4} и b = {4; 3}
• Найдите значение х, при котором векторы a(3;2х;–1), b(2;5;–2). a и b будут ПЕРПЕНДИКУЛЯРНЫ
• Найдите значение х, при котором векторы a(3;2;–1), b(2;х;–2). a и b будут ПАРАЛЛЕЛЬНЫ
• Найдите координаты середины отрезка A = (9;5) В=(7;10)
• Задано распределение двумерной случайной величины. Найти распределения X и Y 0.24
• Задано распределение двумерной случайной величины. Найти безусловные математические ожидания и дисперсии. X и Y
• Найти корреляционный момент случайных величин X и Y, заданных распределением:12-30.15
• Найти коэффициент корреляции случайных величин X и Y, заданных распределением: 0.17 0.1
• Возведите число x = 2 в степень p = \frac 32
• Переведите координаты точки A (4; 1) из декартовой системы координат в полярную:
• Место точки в пространстве координат определяется …
• Из точек А(-2;2), C(2;0), С(9;-5), Р(0;-8) выберите те, которые лежат на оси абсцисс:
• Найти предел последовательности \lim_{n\to\infty}\frac{5n+1}{7-9n} =?
• Какими преобразованиями можно получить график функции y = \sqrt{(x-1)} из графика функции y = \sqrt x?
• Заданы точки: А (-2;1), В(-2; 6), С(2;-5), К(-2;-7). Какой из отрезков параллелен оси ординат?
• Запишите с помощью знака модуля неравенство -3 < x < 3:
• Чему равна длина отрезка AB, если A (8; 2) и B (0; 2):
• Найти расстояние между двумя точками A (12; 1; 1) и B (3; 13; 6):
• Полярный угол j это …
• Если ордината точки равна нулю, то эта точка лежит …
• Какая из точек А(-3; 4), В(2; 2), С(-5;-5), К(-2; 2) лежит на биссектрисе первого координатного угла?
• Выберите верную формулу для нахождения синуса суммы углов?
• Место точки на координатной плоскости определяется …
• Если абсцисса точки равна нулю, то эта точка лежит …
• Выберите верную формулу для нахождения косинуса суммы углов?
• Решите неравенство |x - 1| < 6:
• Какая из точек А(-3; 3), В(3; 3), С(-5;-5), К(2;-2) лежит на биссектрисе второго координатного угла?
• Если С – прямой угол прямоугольного треугольника, и А образует нижний угол \varphi, то {\rm ctg}\varphi вычисляется по формуле:
• Даны два комплексных числа z1=-3i-4 и z2=2i-2. Найдите z1
•z2
• Вычислить сумму z1=-14-5i, z2=7-15i
• Основное свойство мнимой единицы
• Вычислить частное чисел z_1=10-2i, z_2=3+6i
• Вычислить произведение чисел z_1=18-12i, z_2=9+4i
• Показательную форму для комплексного числа позволяет ввести формула…
• Возведение в n-ю степень комплексного числа, заданного в тригонометрической форме производится по формуле:
• Число C = {\rm min}(A) называется минимумом (наименьшим элементом) некоторого подмножества действительных чисел A, если…
• Выберите тригонометрическую форму комплексного числа
• Переведите комплексное число из тригонометрической формы в алгебраическую:
• Переведите комплексное число z = 12 + 5i из алгебраической формы в тригонометрическую:
• При возведении в n-ю степень комплексного числа, заданного в тригонометрической форме
• Выберите верный график функции y=-ln 2x:
• Выберите график логарифмической функции, для которой 0 < a < 1:
• Функции вида y = \sin x называется …
• Выберите верный график функции y=\ln 3x:
• График какой функции получится, если y = \sqrt{3x} перенести на 1 единицу вправо вдоль оси OX и симметрично его отобразить относительно ОХ?
• График какой функции получится, если y = √3x перенести на 1 единицу вправо вдоль оси OX и симметрично его отобразить относительно ОХ?
• При положительных значениях p > 0 степенная функция определена в точке
• При целых значениях p степенная функция определена в области
• График функции y = x^p, где p>1, выглядит следующим образом:
• Выберите верный график функции y=\ln 2x:
• Логарифмическая функция убывает при…
• При возведении в степень показатели степеней
• Исследуйте функцию y=\sqrt x на четность
• Какими преобразованиями получается график функции y= f(-x) из графика функции y=f(x)?
• При любом действительном значении показатели степени p степенная функция определена в области
• Пределом последовательности Ɛ называется …
• Возвести число x в дробную степень p=\frac mn значит…
• Пределом функции y=f(x) в точке x_0 называется …
• Отметьте сходящиеся ряды n+5
• Найдите сумму ряда 5/7
• Найдите сумму ряда 2/7
• Отметьте условно сходящиеся ряды
• Найдите сумму ряда 5/8
• Отметьте абсолютно сходящиеся ряды (n+3)3
• Расстояние |ab| между точками a=M(xa, ya) и b=M(xb, yb) определяется по формуле:
• Расстояние |ab| между точками a=M(x_a, y_a) и b=M(x_b, y_b) определяется по формуле:
• Оси координат разбивают плоскость на четыре части, которые называются …
• Проекции (x_a, y_a) заданной точки на две взаимно перпендикулярные числовые оси Ox и Oy это …
• Если принять начало координат за полюс, а ось Ox за полярную ось, взаимная связь декартовых координат и полярных координат точки может быть выражена следующими формулами:
• Число C = {\rm max}(A) называется максимумом (наибольшим элементом) некоторого подмножества действительных чисел A, если …
• Полюс это …
• Логарифмическая функция возрастает при…
• Логарифмическая функция не существует при…
• Период функции y = ctgx:
• Показательная функция возрастает при…
• Переведите комплексное число z = 4(\cos\pi + i\cdot\sin\pi) из тригонометрической формы в алгебраическую:
• Переведите комплексное число из тригонометрической формы в алгебраическую:
• Величинаsin22x равна:
• Число a называется пределом функции y=f(x) при x стремящемся к бесконечности, если …
• Числовая последовательность это …
• Найти предел функции \lim_{x\to -3}\frac{x^2+2x-3}{x^3+4x^2-3x} =?
• Какая из перечисленных функций является непрерывной на всей числовой прямой?
• Из точек А(-2;0), В(2;0), С(9;-5), Р(0;-8) выберите те, которые лежат на оси абсцисс:
• Абсцисса и ордината заданной точки называются … точки.
• Второй замечательный предел:
• Выберите верное определение понятия график
• Чему равна сумма ряда \sum^5_{n=1}2+2^{n+1}?
• График какой функции получится, если y = x^3 перенести на 5 единицы влево вдоль оси OX?
• При любом действительном значении показателя степени p функция y = x^p определена в области
• Переведите комплексное число z = 6(\cos\frac{5\pi}6 + i\cdot\sin\frac{5\pi}6)из тригонометрической формы в алгебраическую:
• Найдите общий интеграл дифференциального уравнения dy/y=x21dx
• Дано дифференциальное уравнение xy'=y-5 при y(5)=5. Выберите интегральную кривую, которая определяет его решение
• Найдите общий интеграл дифференциального уравнения dy/y6=x7dx
• Дано дифференциальное уравнение xy'=y-10 при y(10)=10. Выберите интегральную кривую, которая определяет его решение
• Дано дифференциальное уравнение y'=4x при y(0)=2. Выберите интегральную кривую, которая определяет его решение
• Найдите решение дифференциального уравнения y'=-6y+2
• Установите соответствие между дифференциальным уравнением и его типом
• Найдите решение дифференциального уравнения y'=-7y+3
• Укажите правильное решение линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами y''+4y'-3y=0
• Определите вид частного решение для неоднородного дифференциального уравнения y''-2y=x+4
• Найдите общий интеграл дифференциального уравнения dy/y4=x7dx
• Укажите правильное решение линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами y''-y'-2y=0
• Производная функции S(t)=-5e5t+3ln6t
• Установите соответствие между дифференциальным уравнением и его типом
• Найдите общий интеграл дифференциального уравнения dy/y=x6dx
• Дано дифференциальное уравнение y'=-x при y(0)=2. Выберите интегральную кривую, которая определяет его решение
• Установите соответствие между дифференциальным уравнением и его типом
• Установите соответствие между дифференциальным уравнением и его типом
• Дано дифференциальное уравнение xy'=y-26 при y(27)=26. Выберите интегральную кривую, которая определяет его решение
• Найдите решение дифференциального уравнения y'=-2y+3
• Определите вид частного решение для неоднородного дифференциального уравнения y''-2y'=5e2x
• Установите соответствие между дифференциальным уравнением и его типом
• Определите вид частного решение для неоднородного дифференциального уравнения y''-5y'=x+1
• В вазе 5 апельсинов, 6 бананов и 7 яблок. Найдите вероятность того, что вынутый фрукт не апельсин
• В вазе 10 яблок, 12 бананов и 8 апельсинов. Найдите вероятность того, что вынутый фрукт не яблоко
• В вазе 13 бананов, 10 яблок и 7 апельсинов. Найдите вероятность того, что вынутый фрукт не банан
• Случайная величина ξ нормально распределена с параметрами a=-10, b=10. С точностью 2 знака после запятой найдите P(ξ<-22)
• Дискретная случайная величина ξ задана таблицей распределения: (-8 6 10)
• Найдите М(ξ) и D(ξ)
• Случайная величина ξ нормально распределена с параметрами a=1, b=15. С точностью 2 знака после запятой найдите P(ξ<-18)
• Случайная величина ξ равномерно распределена на отрезке [-3; 6]. Найдите P(ξ<-1)
• Восстановив недостающее значение, найдите P(ξ<3)
• Дискретная случайная величина задана законом распределения вероятностей:
• Найдите а и b, если её математическое ожидание M= 1,5
• Дискретная случайная величина задана законом распределения вероятностей:
• Случайная величина ξ нормально распределена с параметрами a=-3, b=4. С точностью 2 знака после запятой найдите P(ξ<2)
• Случайная величина ξ задана неполной таблицей распределения: (0 5 6 9)
• Основная гипотеза имеет вид H0: a=17. Определите конкурирующую гипотезу
• Основная гипотеза имеет вид H0: a=7. Определите конкурирующую гипотезу
• Случайная величина ξ нормально распределена с параметрами a=-10, b=20. С точностью 2 знака после запятой найдите P(ξ< -40)
• Случайная величина ξ равномерно распределена на отрезке [1; 2]. Найдите M(ξ) и D(ξ)
• Вероятность сдать тест для Андрея равна 1/3. для Бориса – 3/5. Тест сдал один из них. Найдите вероятность того, что это был Андрей
• Случайная величина ξ нормально распределена с параметрами a=-5, b=6. С точностью 2 знака после запятой найдите P(ξ<-9)
• В урне 14 белых и 7 черных шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что оба будут белыми
• Одновременно бросают 5 монет. Найдите вероятность того, что решками выпадут ровно 3 из них
• Вероятность события А в одном испытании равна 1/2. Найдите вероятность того, что в серии из 6 независимых испытаний событие А произойдет 3 раза
• В урне 12 белых и 8 черных шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что оба будут белыми
• В вазе 9 яблок и 5 бананов. Из вазы вынимают наугад сразу два фрукта. Найдите вероятность того, что хотя бы один из них - яблоко
• Одновременно бросают 7 монет. Найдите вероятность того, что орлами выпадут ровно 6 из них
• В урне 10 чёрных и 20 белых шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что оба будут чёрными
• В урне 10 чёрных и 20 зеленых шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что они будут разного цвета
• В урне 10 желтых и 14 синих шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что оба будут желтыми
• Вероятность события А в одном испытании равна 3/4. Найдите вероятность того, что в серии из 4 независимых испытаний событие А произойдет 2 раза
• Вероятность события А в одном испытании равна 1/2. Найдите вероятность того, что в серии из 8 независимых испытаний событие А произойдет 6 раз
• Детали поступают на общий конвейер от двух станков, производительности которых относятся как 2:1. Вероятность изготовления качественной детали для этих станков равны соответственно 3/4 и 2/3. Наудачу взятая деталь оказалась качественной. Найти вероятность того, что она изготовлена на первом станке
• Вероятности независимых событий А и В равна соответственно 1/2 и 4/5. В результате испытания произошло ровно одно из них. Найдите вероятность того, что это было событие А
• Имеется 12 винтовок с оптическим прицелом и 6 винтовок без оптического прицела. Вероятность поражения мишени из винтовки с оптическим прицелом равна 9/10 , без оптического прицела - 1/2. Из случайно взятой винтовки цель поражена. Найти вероятность того, что была взята винтовка с оптическим прицелом
• Вероятности независимых событий А и В равна соответственно 6/7 и 2/3. В результате испытания произошло ровно одно из них. Найдите вероятность того, что это было событие А
• Всхожесть моркови составляет 50%, свеклы – 30%. В лаборатории посадили по одному семени каждого овоща. Взошел один росток. Найти вероятность, что это свеколка
• Всхожесть моркови составляет 50%, свеклы – 80%. В лаборатории посадили по одному семени каждого овоща. Взошел один росток. Найти вероятность, что это морковка
• В вазе 13 бананов, 7 апельсинов и 8 яблок. Найдите вероятность того, что вынутый фрукт не банан
• В урне 12 желтых и 10 белых шаров. Из урны вынимают наугад сразу два шара. Найдите вероятность того, что оба будут желтыми
• Вероятность события А в одном испытании равна 3/4. Найдите вероятность того, что в серии из 3 независимых испытаний событие А произойдет 2 раза
• Вероятность сдачи теста для Андрея равна 4/5. для Бориса – 1/3. Тест сдал один из них. Найдите вероятность того, что это был Борис
• Случайная величина ξ нормально распределена с параметрами a=-2, b=20. С точностью 2 знака после запятой найдите P(4ξ-42<0)
• Детали поступают на общий конвейер от двух станков, производительности которых относятся как 1:2. Вероятность изготовления качественной детали для этих станков равны соответственно 3/5 и 7/10. Наудачу взятая деталь оказалась качественной. Найти вероятность того, что она изготовлена на первом станке
• Случайная величина ξ нормально распределена с параметрами a=-10, b=5. С точностью 2 знака после запятой найдите P(ξ< -17)
• Случайная величина ξ нормально распределена с параметрами a=9, b=19. С точностью 2 знака после запятой найдите P(4ξ+46<0)
• Детали поступают на общий конвейер от двух станков, производительности которых относятся как 5:7. Вероятность изготовления качественной детали для этих станков равны соответственно 2/3 и 4/7. Наудачу взятая деталь оказалась качественной. Найти вероятность того, что она изготовлена на первом станке
• Случайная величина ξ нормально распределена с параметрами a=10, b=10. С точностью 2 знака после запятой найдите P(4ξ -23<0)
• Дискретная случайная величина ξ задана таблицей распределения: (-6 7 8)
• При одном выстреле танк поражает цель с р = 0,8. Найти вероятность Р, что при трех выстрелах первые две цели будут поражены, а третий выстрел – мимо.
• Каждый год из 100 выпускников факультета ВУЗа в среднем в аспирантуру поступают 2 выпускника ВУЗа. Найти вер. Р, что в этом году из 100 выпускников в аспирантуру поступят 3 выпускника.
• Футбольная команда играет поочередно матч дома и матч на выезде. Команда выигрывает домашний матч с р1 = 0,7 , на выезде с р2 = 0,5. Найти вероятность Р, что текущий матч команда выиграет.
• Гонщик, как правило, выигрывает одну автогонку с вероятностью р = 0,2. Определить вероятность Р, что из двух следующих гонок он не выиграет ни одну гонку.
• В пустыне Гоби в год падает примерно 730 метеоритов. Найти вероятность Р, что завтра в пустыне упадет ровно 1 метеорит.
• В шахматном турнике студент играет половину партий белыми и половину партий черными фигурами. Белыми он выигрывает партию с р1 = 0,7, черными фигурами с р2 = 0,4. Найти P, что он выиграет текущую партию.
• Каждая сотая деталь, выпускаемая в цехе, бракованная. Найти вероятность Р, что в партии из 200 деталей 2 детали – брак.
• Зенитная установка сбивает самолет одним выстрелом с р = 0,6. Найти вероятность Р , что в случае четырех выстрелов по эскадрильи зенитная установка собьет ровно 2 самолета.
• Белый олень рождается в каждом 100-ом случае. Найти Р, что среди в этом году среди 200 новорожденных оленей родится ровно 2 альбиноса.
• Игрок бросает 2 игральные кости на стол. Найти вероятность Р, что выпадет ровно 10 очков.
• В коробке 2 синих и 3 черных карандаша. Найти вероятность Р, что при случайном выборе из коробки 3 карандашей - 1 окажется синим и 2 черными.
• Тигр-альбинос рождается в каждом 200-ом прайде. Найти Р, что среди 400 прайдов в саване родится ровно 3 тигра.
• В кошельке 2 золотые монеты и 4 серебряные. Найти вероятность Р, что при случайном выборе из кошелька 3 монет - 1 окажется золотой и 2 серебряные.
• Время Т ремонта машины в автосервисе - непрерывная СВ и Найти вероятность Р, что СВ T примет значение от 0 до 2.
• Непрер. случайная величина Х имеет функцию плот. вероятности:
• Найти вероятность, что случ. величина Х примет значение от 0 до 2.
• В бак машины входит в среднем М(Х) = 20 л бензина. При этом дисперсия этой случайной величины равна D(X) = 4 л2 . Найти вероятность Р, что в бак войдет от 19 до 21 л. Здесь Ф(0,5) = 0,19.
• Определить математическое ожидание М(Х) этой СВ Х.
• Объем сбыта продукции Q фирмы зависит от числа N её торговых точек. Чему примерно будут равны коэфф. корреляции RQN:
• В результате обработки стат. данных построена регрессионная модель П = 400 + 5* t зависимости прибыли предприятия П от месяца t с начала прошедшего года до его конца ( t = 1, 2, .. 12). Сделать прогноз прибыли П на март следующего года:
• На испытаниях трактор показал скорости: V = ….. 56 , 58, 60, 62 , 64 … км/ч . Найти вер. Р, что в полевых условиях он покажет от 59 до 61 км/ч. Здесь Ф(0,32) 0,13:
• При измерении температуры Т в мае получены следующие значения : Т = ……. 18, 19, 20, 21 , 22 … (С° ) . Найти вер. Р, что при контрольном измерении будет получена температура в пределах 21 < Т < 22 , С°. Здесь Ф(1,27)≈ 0,4 , Ф/(0,63)≈ 0,24.
• В среднем на каждой сотой странице книги – опечатка. Найти вероятность Р того , что на 200 страницах книги встретятся ровно 3 опечатки.
• На полке стоят 2 книги по физике и 3 книги по экономике. Случайным образом с полки снимают 3 книги. Найти вероятность Р, что это будут 1 книга по физике и 2 книги по экономике.
• В пирамиде стоят 5 винтовок, из них две имеют оптический прицел. Вероятность, что цель будет поражена из обычной винтовки р1=0,8, а из винтовки с оптическим прицелом р2 = 0,9.
• Лидер велотура в среднем побеждает в каждой третьей гонке. Найти вероятность Р, что в трех предстоящих гонках велотура он победит ровно 2 раза.
• В коробке 3 нормальны и 2 бракованные лампочки. Случайным образом одна лампочка разбилась. Найти вероятность Р, что случайно взятая из коробки лампочка – брак.
• Лучник попадает в цель одним выстрелом с р = 0,8. Найти вероятности, что в случае четырех выстрелов он попадет в цель ровно 2 раза.
• Производная функции S(t)=6cos5t-3tg2t равна
• Производная функции V(t)=-2e2t+5ln6t равна
• Найдите множество первообразных функций f(x)=-sin(2x-4)
• Найдите множество первообразных функций f(x)=-cos(5x+2)
• Интеграл -п/6S-п/2
• Интеграл -п/6S-п
• Частные производные первого порядка функции z=cos(x4/y6) равны:
• Частная производная второго порядка функции z=3xy2+5y/x+7равна:
• Производная функции y(x)=4/5x3-1/5x2+1/5x-3/4 равна:
• Найдите и запишите точку перегиба функции
• y=x3 -24x2 +2x-1
• Укажите условия сходимости условно знакопеременного ряда
• Восстановить соответствие между неопределенными интегралами или производной с их значением:
• Найдите и запишите точку максимума функции
• y=-x2 -12x+4.
• Установить соответствие между функциями и их предельным значением:
• Вычислите предел функции
• Установите соответствие между последовательностями и формулой общего члена этой последовательности:
• Вычислите значение производной в точке x0=1 функции
• y = x5 – x4 + x3 – x2 + x – 5
• Укажите сходимость ряда u4+ u5+…+ un+…, если известно, что ряд u1+ u2+ u3+…+ un+… сходится.
• Установите соответствие между формулами для нахождения асимптот и видом асимптот графика функции y=f(x):
• Вычислите предел числовой последовательности:
• Установите соответствие между функциями и их производными:
• Вычислите предел функции
• Выберите вид производной функции
• Укажите значение второй производной f''(x), которое соответствует выпуклости функции вверх на интервале (a, b).
• Установить соответствие между функцией и одной из её асимптотой:
• Выберите правильный вариант ответа. Чему равен угловой коэффициент касательной, проведенной к графику функции в некоторой точке?
• Вычислите производную функции y=20x+5
• Вычислите значение определенного интеграла
• Вычислите предел числовой последовательности:
• Установите соответствие между изображениями операциями над множествами A и B и названиями этих операций:
• Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию y(4) = 1:
• Найти общее решение дифференциального уравнения:
• Найти частное решение дифференциального уравнения,
• удовлетворяющее начальным условиям y(0) = 2, y’(0) = 2:
y’’ – (y’)2+ y’ (y - 1) = 0
• Найти общее решение линейного обыкновенного
дифференциального уравнения y’’ - 6 y’ + 25 y = 0
• Вычислить матричное выражение A 2+3·A+5·E для следующей
матрицы A:
• Вычислить произведение матриц A·B:
• Вычислить определитель матрицы A, выполнив разложение по строке или по столбцу:
• Найти ранг матрицы A
• Решить систему линейных уравнений с помощью обратной матрицы:
• Решить систему линейных уравнений методом Крамера:
• Решить систему линейных уравнений методом Гаусса:
• Решить систему линейных уравнений методом Жордана-Гаусса
• Решить систему линейных уравнений с помощью обратной матрицы:
• Решить систему линейных уравнений методом Крамера:
• Решить систему линейных уравнений методом Гаусса:
• Решить систему линейных уравнений методом Жордана-Гаусса:
• Вычислите значение определенного интеграла
• Выберите правильный вариант ответа. Указать числовой промежуток, на котором определена функция
• Установите соответствие между функциями и характеристиками этих функций:
• Найдите сумму главной диагонали матрицы, полученной путём произведения матриц
• Вычислите определитель матрицы
• Определите длину вектора с координатами {2; 2; 2 ;2}:
• Укажите, какие из нижеперечисленных матриц второго порядка являются треугольными
• Пусть две строки матрицы поэлементно равны между собой. Вычислите, чему равен ее определитель.
• Укажите, какие из нижеперечисленных матриц третьего порядка являются треугольными
• Вычислите сумму элементов главной диагонали матрицы
• Соотнесите дифференциальные уравнения (ДУ) и их типы.
• На плоскости рассматриваются два базиса: старый и новый . Укажите какой будет матрица перехода от старого базиса к новому Соотнесите:
• Вычислите определитель матрицы
• Пусть дифференциальное уравнение является многочленом относительно старшей производной. Укажите, как называется степень этого многочлена:
• Дана матрица
• Соотнесите элемент матрицы с его значением:
• Соотнесите произведение матриц А*B:
• Выберите справедливые утверждения для графиков линейных функций.
• Вычислите значение параметра m, при котором векторылинейно зависимы:
• Укажите, какие из нижеперечисленных матриц второго порядка являются диагональными (несколько вариантов)
• Вычислите скалярное произведение двух векторов с координатами {2; 3; 1} и {-1; 0; 4}:
• Вычислите длину вектора с координатами {3; 4}:
• Определите, при каком значении а система линейных уравнений несовместна:
• Вычислите определитель
• Укажите, какие из следующих наборов векторов на плоскости являются линейно зависимыми?
• Вычислите, при каком х определитель равен 24.
• Укажите, какие из нижеперечисленных матриц третьего порядка являются диагональными
• Вычислите длину вектора с координатами {4; -3}:
• Соотнесите матрицу и её вид:
• Укажите, какие из следующих наборов векторов в пространстве являются линейно зависимыми
• Найдите сумму x 1 +x 2 +x 3 , где (x 1 , x 2 , x 3 ) - решение системы:
• Соотнесите ранг матрицы с соответствующим ему значением:
• Вычислите определитель матрицы
• Укажите тип дифференциального уравнения, в котором содержится функция от одной переменной:
• Вычислите определитель матрицы
• Укажите решения, которые можно получить при решении дифференциальных уравнений:
• Укажите тип дифференциального уравнения, которое содержит неизвестные функции нескольких переменных и их частные производные:
• Пусть ненулевые векторы линейно зависимы, тогда выберите верные утверждения (несколько вариантов):
• Вычислите сумму элементов второй строки транспонированной матрицы АТ
• Соотнесите термин с соответствующим ему определением:
• Вычислите скалярное произведение векторов с координатами {1; 2} и {1; -3}:
• Укажите, каких из нижеперечисленных условий достаточно, чтобы скалярное произведение векторов равнялось нулю
• Найдите сумму x 1 +x 2 +x 3 , где (x 1 +x 2 +x 3 ) - решение системы:
• Выберите верные утверждения (высказывания).
• Укажите класс дифференциальных уравнений первого порядка, которые наиболее легко поддаются решению и исследованию:
• Вычислите определитель произведения матриц A•A T (произведение матрицы и транспонированной к ней)
• Найдите расстояние между точками A(0, -3, 3) и B(3, 1, 3).
• Пусть А, В – матрицы размерности 2х2. Выберите, какие из нижеперечисленных утверждений верны.
• Укажите, какие из следующих наборов векторов на плоскости являются линейно зависимыми
• Определите угловой коэффициент прямой х – у + 5 = 0:
• Соотнесите действие над матрицами и результат:
• Найдите ранг матрицы
• Определите ранг матрицы
• Определите элемент k23 транспонированной матрицы КT
• Вычислите определитель матрицы:
• Два вектора в евклидовом пространстве ортогональны. Чему равно их скалярное произведение.
• Определите длину вектора с координатами {6; 6; 7}
• Определите, при каком λ матрица вырождена:
• Известно, что матрица имеет размерность 2х2 и detA=-3. Вычислите, чему равен det(-4*A)?
• Произведение матриц А•В определено, если… (несколько вариантов)
• Вычислите определитель Δ1 в формуле Крамера для системы линейных уравнений
• При перестановке двух строк матрицы определитель умножается на это число
• При транспонировании матрицы ее Определитель меняет знак
• При умножении всех элементов некоторой строки матрицы на число определитель исходной матрицы не меняется
• Соотнесите начало и конец утверждения:
• Вычислите определитель матрицы коэффициентов системы уравнений:
• Установите, чему будет равен предел если известно, что
• Установите соответствие между точкой x i и непрерывностью функции в этой точке:
• Укажете формулу «второго замечательного предела»:
• Вычислите производную функции y = 5 x - 2
• Выберите вид производной функции y=sin4 5x
• Выберите вид производной функции y = x4 ·e5x
• Выберите правильный вариант ответа. Определить точки разрыва функции, указать какого они типа.
• Вычислите значение второй производной функции y = 5x2 + 50x + 100
• Укажите, чему равен градиент функции в точке минимума.
• Укажите значение второй производной f '' (x), которое соответствует выпуклости функции вниз на интервале (a, b).
• Вычислите предел числовой последовательности
• Вычислите предел функции
• Выберите вид производной функции y = x6 • sin2x.
• Чему будет равна производная функции y=e2x-4 в точке x=2?
• Найдите и запишите точку локального минимума функции y = 2 x3 - 24 x + 3 на интервале (-5; 5).
• Укажете формулу «первого замечательного предела»:
• Выберите правильный вариант ответа. Определить точки разрыва функции, указать какого они типа.
• Укажите значение второй производной f ''(x), которое соответствует выпуклости функции вверх на интервале (a, b).
• Найдите и запишите точку максимума функции y = -x2 – 12 x + 4.
• Вычислите значение определенного интеграла
• Вычислите предел функции:
• Вычислите значение несобственного интеграла
• Выберите правильный вариант ответа. Объединение множеств А и В – это...
• Найдите число элементов разности множеств А \ В, если А={31, 32, 34, 35} и В ={30, 34, 35, 36}
• Выберите правильный вариант ответа. К какому типу принадлежит последовательность |an|, заданная формулой n–го члена an = (-2)n ?
• Выберите правильный вариант ответа. Указать числовой промежуток, на котором определена функция
• Выберите выражение, которое соответствует второй частной производная z"xy для функции z = xy2 + ex
• Выберите правильный вариант ответа. К какому типу принадлежит последовательность |an|, заданная формулой n–го члена
• Вычислите сумму элементов первого столбца матрицы C=2•A-B.
• Даны координаты точек: А(11; 8), В(7; 5). Вычислите длину вектора AB:
• На плоскости рассматриваются два базиса: старый и новый . Укажите какой будет матрица перехода от старого базиса к новому Соотнесите:
• Укажите, что является порядком дифференциального уравнения:
• Вычислите определитель произведения двух матриц
• Вычислите определитель матрицы
• Назовите уравнение, которое помимо функции содержит её производные.
• Найдите ранг матрицы
• Соотнесите действие с результатом:
• Определите длину вектора с координатами {2; 2; 1}.
• Вычислите скалярное произведение векторов с координатами {7;3; 4} и {-1; 1; 1}:
• Вычислите координаты вектора по заданным точкам и соотнесите с результатом:
• Соотнесите формулу с её символьным представлением:
• Вычислите сумму элементов побочной диагонали матрицы
• Вычислите определитель матрицы Δ системы линейных уравнений:
• Найдите расстояние между точками A(-3, 3, 3) и B(1, 3, 0).
• Вычислите сумму элементов первой строки матрицы, которая получится в результате произведения матриц A•B:
• Вычислите определитель матрицы
• Прямая имеет уравнение 2х – 5у + 7 = 0. Укажите, какие из нижеперечисленных векторов являются направляющим вектором данной прямой в декартовой системе координат.
• Вычислите скалярное произведение векторов с координатами {1;2;3;6;4} и {12;6;4;2;3}
• Соотнесите минор матрицы
• Вычислите длину вектора с координатами {-4; -3}:
• Вычислите произведение элементов побочной диагонали матрицы
• Вычислите произведение элементов главной диагонали результирующей матрицы C=A+B.
• Вычислите скалярное произведение векторов с координатами {1;1;0;1;-1} и {2;0;2;0;2}:
• Вычислите скалярное произведение векторов с координатами {1; 2; 0; -4} и {-2; 3; 0; 1}:
• Вычислите произведение элементов второй строки матрицы, которая получится в результате произведения матриц A•B:
• Вычислите определитель Δ3 в формуле Крамера для системы линейных уравнений
• Вычислите скалярное произведение двух векторов с координатами {-1; 0; 2} и {4; 3; 1}:
• Вычислите сумму элементов главной диагонали матрицы, которая получится в результате суммы двух матриц:
• Вычислите сумму элементов первого столбца матрицы, которая получится в результате произведения A•B.
• Вычислите произведение элементов побочной диагонали матрицы, которая получится в результате суммы двух матриц:
• Вычислите скалярное произведение векторов с координатами {7; 3; 4} и {-1 ;1; 1}:
Ответы на некоторые вопросы по тесту.
Проверенные ответы на тест
+ a. Неограниченная
b. Возрастающая
c. Ограниченная
d. Убывающая
a.5 элементов
b.3 элемента
+ c.2 элемента
d.4 элемента
a.5 элементов
b.4 элемента
c.6 элементов
+ d.3 элемента
a.1
+ b.13
c.-5
d.5
e.0
a. Убывающая
+ b. Неограниченная
c. Возрастающая
d. Ограниченная
a.-12
b.4
+ c.-6
d.0

Ответ на промежуточный тест ММУ

Ответ на промежуточный тест ММУ

Ответ на промежуточный тест ММУ


Производная функция

Производная функция

Найдите множество первообразных функций
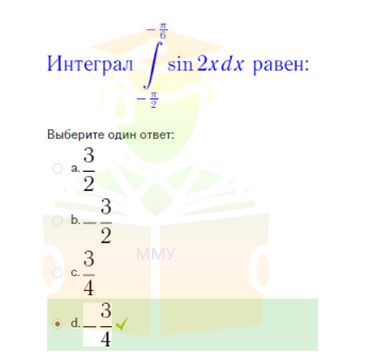
Интеграл равен

Величина равна

Отметьте сходящиеся ряды

Отметьте абсолютно сходящиеся ряды

Вычислите частные производные функции

Частные производные первого порядка функции равны

Определите вид частного решения для неоднородного дифференциального уравнения

Укажите правильное решение линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами

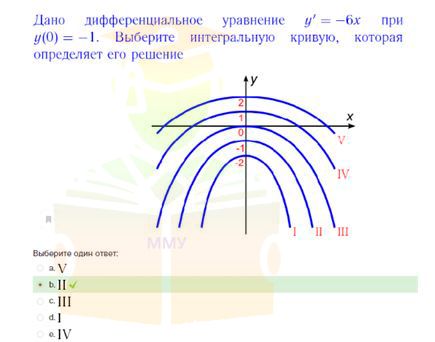
Дано дифференциальное уравнение y'=-6x при y(0)=-1. Выберите интегральную кривую, которая определяет его решение
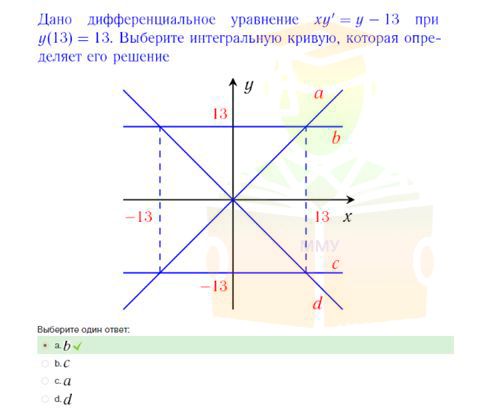
Дано дифференциальное уравнение xy'=y-13 при y(13)=13. Выберите интегральную кривую, которая определяет его решение

Установите соответствие между дифференциальными уравнениями и его типом

Найдите решение дифференциального уравнения
Проверенные ответы на задачи.
Тест-Вероятность и Испытание Бернули
Ответ на задачу: 40/77
Ответ на задачу: 43/91
Ответ на задачу: 13/38
Ответ на задачу: 21/38
Ответ на задачу: 7/9
Ответ на задачу: 5/16
на этой странице, вы сможете оставить заявку
НАШИ КОНТАКТЫ