Список некоторых  вопросов из тестов, на которые мы можем помочь с ответами. 

• Кривая закона распределения характеризует.

• Для определения тесноты связи двух альтернативных показателей применяют:

• Среднее выборочное вариационного ряда 1; 2; 3; 3; 7; 8 равно …

• Статистический индекс - это:

• По какой формуле производится вычисление средней величины в интервальном ряду.

• Повторный отбор отличается от бесповторного тем, что:

• Назовите основные организационные формы статистического наблюдения:

• Статистический показатель - это.

• Средняя геометрическая - это:

• Значения признака, повторяющиеся с наибольшей частотой, называется.

• Трендом ряда динамики называется:

• Сумма всех удельных весов показателя структуры.

• При каком значении линейного коэффициента корреляции связь между X и Y можно признать более существенной:

• Анализ взаимосвязи в статистике исследует:

• Дана выборка 6; 7; 0; -2; 5; 1; -1; 5. Тогда её выборочная медиана равна …

• Средний уровень интервального ряда динамики определяется как:

• Размах вариации исчисляется как.

Может ли индекс переменного состава превышать индекс фиксированного

• состава:

• Может ли в отдельных случаях средний гармонический индекс рассчитываться по средней гармонической невзвешенной:

• Прогнозирование в статистике - это:

• Можно ли утверждать, что индивидуальные индексы по методологии исчисления адекватны темпам роста:

• Что понимается в статистике под термином «вариация показателя».

• Могут ли взвешенные и невзвешенные средние, рассчитанные по одним и тем же данным, совпадать.

• Группировочные признаки, которыми одни единицы совокупности обладают, а другие - нет, классифицируются как:

• Укажите показатели вариации.

• Статистический показатель дает оценку свойства изучаемого явления:

• Статистические показатели по сущности изучаемых явлений могут быть: а) качественными б) объёмными.

• Для выявления основной тенденции развития используется: а) метод укрупнения интервалов; б) метод скользящей средней; в) метод аналитического выравнивания; г) метод наименьших квадратов;

• Показатель дисперсии - это:

• Закон больших чисел утверждает, что:

• Выборочная совокупность отличается от генеральной:

• Статистическая связь - это:

• Необходимая численность выборочной совокупности определяется:

• Как изменяется средняя арифметическая, если все веса уменьшить в А раз.

• Дана выборка 1,91; 1,88; 1,95; 1,96; 1,92; 1,90; 1,93. Тогда её выборочная медиана равна …

• Медиана в ряду распределения с четным числом членов равна.

• Термин корреляция в статистике понимают как:

• Какой коэффициент корреляции характеризует связь между X и Y:

• Коэффициент вариации измеряет колеблемость признака.

• Статистическое наблюдение – это:

• Ошибка репрезентативности относится к:

• Ошибка репрезентативности обусловлена:

• Размах вариации исчисляется как.

• Статистическая группировка - это:

• Ряд динамики, характеризующий уровень развития социально-экономического явления на определенные даты времени, называется:

• Термин регрессия в статистике понимают как: а) функцию связи, зависимости; б) направление развития явления вспять; в) функцию анализа случайных событий во времени; г) уравнение линии связи.

• К каким группировочным признакам относятся: образование сотрудников, профессия бухгалтера, семейное положение:

• Статистические показатели в зависимости от характера изучаемых явлений могут быть: а) интервальными б) моментными.

• Среднеквадратическое отклонение характеризует.

• Как изменится средняя арифметическая, если все значения определенного признака увеличить на число А.

• К каким группировочным признакам относятся: сумма издержек обращения, объем продаж, стоимость основных фондов.

• Средне квадратическое отклонение исчисляется как.

• Коэффициент доверия в выборочном методе может принимать значения:

• Индексы позволяют соизмерить социально-экономические явления:

• Основными задачами статистики на современном этапе являются: а) исследование преобразований экономических и социальных процессов в обществе; б) анализ и прогнозирование тенденций развития экономики; в) регламентация и планирование хозяйственных процессов;

• Малая выборка - это выборка объемом:

• Статистическая сводка - это:

• Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените.

• Статистика как наука изучает:

• Ряд распределения - это:

• При каком значении коэффициента корреляции связь можно считать умеренной:

• Средняя ошибка выборки:

• Статистика изучает явления и процессы посредством изучения:

• Средняя хронологическая исчисляется.

• Исчисление средних величин - это.

• Выборка может быть: а) случайная, б) механическая, в) типическая, г) серийная, д) техническая.

• Дайте классификацию связей по аналитическому выражению:

• В каких единицах будет выражаться относительный показатель, если база сравнения принимается за единицу.

• Является ли статистическим наблюдением наблюдения покупателя за качеством товаров или изменением цен на городских рынках.

• Абсолютный прирост исчисляется как: а) отношение уровней ряда; б) разность уровней ряда. Темп роста исчисляется как: в) отношение уровней ряда; г) разность уровней ряда;

• Анализ взаимосвязи в статистике исследует:

• К наиболее простым методам прогнозирования относят:

• Статистическая совокупность – это:

• По направлению связь классифицируется как: 

 • Непрерывная двумерная случайная величина распределена внутри прямоугольного треугольника с вершинами О (0;0), А(0;-6), В(-6;0). Найти плотность системы. 

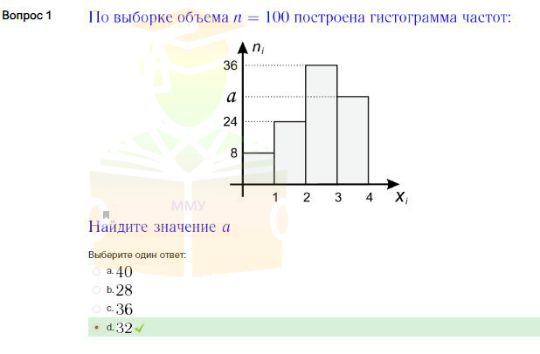
• По выборке объема n=100 построена гистограмма частот: 

• В результате пяти проведенных измерений некоторой случайной величины (без систематических ошибок) получены следующие результаты (в мм): 7, 14, 15, 16, 17. Определите несмещенную оценку математического ожидания

 • Задано распределение двумерной случайной величины. Найти распределения X и Y. (0,09 0,01 0,23) 

 • Непрерывная двумерная случайная величина распределена внутри прямоугольного треугольника с вершинами О (0;0), А(0;-13), В(-13;0). Найти плотность системы.

 • Непрерывная двумерная случайная величина распределена внутри прямоугольного треугольника с вершинами О (0;0), А(0;2), В(2;0). Найти плотность системы. 

• Задано распределение двумерной случайной величины. Найти безусловные математические ожидания и дисперсии. (0,01 0,21 0,17)

• Найти коэффициент корреляции случайных величин X и Y, заданных распределением: (0,17 0,1 0,01) 

• Найти корреляционный момент случайных величин X и Y, заданных распределением: 

•   Выберите значения, которые может принимать выборочный коэффициент корреляции 

  • Выборочное уравнение прямой регрессии имеет вид у = 1,8х -4. Выберите значения, которые может принимать выборочный коэффициент корреляции 

 • В результате пяти проведенных измерений некоторой случайной величины (без систематических ошибок) получены следующие результаты (в мм): 7, 16, 17, 18, 19. Определите несмещенную оценку математического ожидания